Bài tập về sóng dừng

BÀI TẬP VỀ SÓNG DỪNG

Bài 1: Trên một sợi dây đàn hồi AB dài 25cm đang có sóng dừng, người ta thấy có 6 điểm nút kể cả hai đầu A và B. Hỏi có bao nhiêu điểm trên dây dao động cùng biên độ, cùng pha với điểm M cách A 1cm?

A. 10 điểm                            B. 9                            C. 6 điểm                           D. 5 điểm

Giải

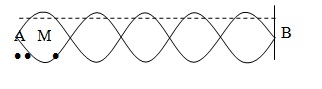
l = k \(\frac{\lambda }{2}\)----> 25 = 5 \(\frac{\lambda }{2}\) -----> λ = 10 cm

Biểu thức của sóng tại A là

u_A = acosωt

Xét điểm M trên AB:   AM = d  ( 1≤ d ≤25)

Biểu thức sóng tổng hợi tại M

u_M= 2asin\(\frac{2\pi d}{\lambda }\) cos(ωt + \(\frac{\pi }{2}\)).

Khi d = 1cm: biên độ a_M = 2asin\(\frac{2\pi d}{\lambda }\) = 2asin\(\frac{2\pi .1}{10}\)= 2asin\(\frac{\pi }{5}\)

Các điểm dao độngs cùng biên độ và  cùng pha với M

  sin \(\frac{2\pi d}{\lambda }\) = sin \(\frac{\pi }{5}\)

  -----> \(\frac{2\pi d}{\lambda }\) = \(\frac{\pi }{5}\) + 2kπ  ----> d₁ =  1 + 10k_{1­ ;}   1≤ d₁ = 1 + 10k_1­ ≤ 25----> 0 ≤ k₁ ≤2:  có 3 điểm

            \(\frac{2\pi d}{\lambda }\) = \(\frac{4\pi }{5}\) + 2kπ------> d₂ = 4 + 10k₂ ; 1≤ d₁ = 4 + 10k_2­ ≤ 25----> 0 ≤ k₂ ≤2: có 3 điểm

Như vậy ngoài điểm M còn 5 điểm dao động cùng biên độ, cùng pha với điểm M.

 đáp án D

Bài 2. :Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây A là một điểm nút, B là một điểm bụng gần A nhất, AB = 14 cm, gọi C là một điểm trong khoảng AB có biên độ bằng một nửa biên độ của B. Khoảng cách AC là

A.14/3                           B.7                             C.3.5                            D.1.75

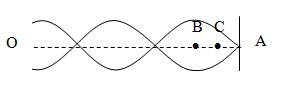
Giả sử biểu thức sóng tại nguồn O (cách A: OA = l.) u = acosωt

Xét điểm C cách A:   CA = d. Biên độ của sóng dừng tai C   a_C = 2asin\(\frac{2\pi d}{\lambda }\)

Để a_C = a  (bằng nửa biện độ của B là bụng sóng):  sin\(\frac{2\pi d}{\lambda }\)= 0,5

 -----> d = ( \( \frac{1}{12}\)+ k)λ . Với λ = 4AB = 56cm. Điểm C gần A nhất ứng với k = 0

d = AC = λ/12 = 56/12 = 14/3 cm.

đáp án A 

Bài 3: Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất với AB = 18 cm, M là một điểm trên dây cách B một khoảng 12 cm. Biết rằng trong một chu kỳ sóng, khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc cực đại của phần tử M là 0,1s. Tốc độ truyền sóng trên dây là:
A. 3,2 m/s.                       B. 5,6 m/s.                           C. 4,8 m/s.                          D. 2,4 m/s.

Giải: 

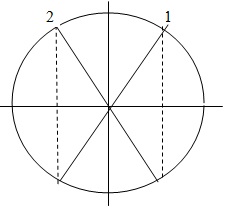
AB = \( \frac{\lambda }{4}\) = 18cm-----> λ = 72 cm

Biểu thức của sóng dừng tại điểm M cách nút A,  AM = d

    u_M = 2acos(\(\frac{2\pi d}{\lambda }\) + \(\frac{\pi }{2}\) )cos(ωt - kπ - \(\frac{\pi }{2}\) )

Khi AM = d = \( \frac{\lambda }{6}\) 

 u_M = 2acos( \( \frac{2\pi \lambda }{6\lambda }\) + \(\frac{\pi }{2}\) )cos(ωt - kπ- \(\frac{\pi }{2}\) )  = 2acos( \( \frac{\pi }{3}\)+ \(\frac{\pi }{2}\))cos(ωt - kπ- \(\frac{\pi }{2}\)  )

u_M = - 2asin(\( \frac{\pi }{3}\) )cos(ωt - kπ- \(\frac{\pi }{2}\))

v_M =  2aω\( \frac{\sqrt{3}}{2}\)sin(ωt - kπ- \(\frac{\pi }{2}\) )------>   v_M =  aω\( \sqrt{3}\)sin(ωt - kπ - \(\frac{\pi }{2}\) )------>v_Mmax = aω\( \sqrt{3}\)

u_B = 2acos(ωt - kπ- \(\frac{\pi }{2}\) )  ------> v_B = -2aωsin(ωt - kπ- \(\frac{\pi }{2}\) )------>

| 2aωsin(ωt - kπ- \(\frac{\pi }{2}\) )| <  aω\( \sqrt{3}\) -------> | sin(ωt - kπ-  \(\frac{\pi }{2}\))| < \( \sqrt{3}\) /2

| cos(ωt - kπ) | < \( \sqrt{3}\)/2  = cos\( \frac{\pi }{3}\)

Trong một chu kì khoảng thời gian mà độ lớn

vận tốc dao động của phần tử B nhỏ hơn vận tốc

cực đại của phần tử M là t = 2t₁₂ = 2x T/6 = T/3 = 0,1s

Do đó T = 0,3s -------->Tốc độ truyền sóng v = \( \frac{\lambda }{T}\) = 72/0,3 = 240cm/s = 2,4m/s

đáp án D