Cực trị xác định giá trị cực đại của điện áp hiệu dụng khi thay đổi thông số mạch

CỰC TRỊ XÁC ĐỊNH GIÁ TRỊ CỰC ĐẠI CỦA ĐIỆN ÁP HIỆU DỤNG KHI THAY ĐỔI THÔNG SỐ CỦA MẠCH 

1.Các công thức của các điện áp hiệu dụng cực đại khi thông số của mạch thay đổi:

a. Điện áp hiệu dụng U_R:

+ R thay đổi : U_R(max) = U  Khi R →∞ 

+ L,hay C, hay ω  thay đổi :  U_R(max) = U  Khi \(\omega =\frac{1}{\sqrt{LC}}\)   ( Cộng hưởng )

b. Điện áp hiệu dụng : U_L

+ R thay đổi :  U_L(max) = \(\frac{U}{\left | Z_{L}-Z_{C} \right |}Z_{L}\)  khi R = 0

+ L thay đổi :   U_L(max) = IZ_L = \(\frac{U\sqrt{R^{2}+{Z_{C}}^{2}}}{R}\)   khi Z_L = \(\frac{R^{2}+{Z_{C}}^{2}}{Z_{C}}\)

+ C thay đổi :   U_L(max) = IZ_L  = \(\frac{U}{R}Z_{L}\)     khi C =  \(\frac{1}{L\omega ^{2}}\)( Cộng hưởng )

+  thay đổi :  U_L(max) = IZ_L    khi  \(\omega =\sqrt{\frac{2}{2LC-R^{2}C^{2}}}\)

c. Điện áp hiệu dụng : U_C

+ R thay đổi :  U_C(max) = \(\frac{U}{\left | Z_{L}-Z_{C} \right |}Z_{C}\)   khi R = 0

+ C thay đổi :   U_C(max) = IZ_C = \(\frac{U\sqrt{R^{2}+{Z_{L}}^{2}}}{R}\)  khi Z_C = \(\frac{R^{2}+{Z_{L}}^{2}}{Z_{L}}\)

+ L thay đổi :   U_C(max) = IZ_C  =  \(\frac{U}{R}Z_{C}\)     khi L = \(\frac{1}{C\omega ^{2}}\)  ( Cộng hưởng )

+  thay đổi :  U_C(max) = IZ_C    khi  \(\omega =\sqrt{\frac{1}{LC}-\frac{R^{2}}{2L^{2}}}\)

2. Công thức thường gặp cần nhớ khi L,C, f  thay đổi  (không Cộng hưởng):

Tìm L để U_Lmax:( Mạch điện hình vẽ bên phải khi L thay đổi)

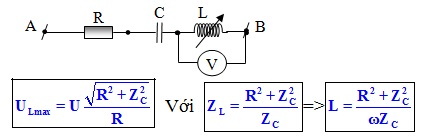
Tìm C để U_Cmax:( Mạch điện hình vẽ bên phải khi C thay đổi)

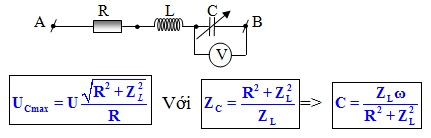
Xác định giá trị cực đại U_Lmax, và U_Cmax khi tần số f  thay đổi:

         (với điều kiện  \(2\frac{L}{C}> R^{2}\))

3. Bài tập về xác định giá trị cực đại U_max khi thay đổi L, hoặc C, hoặc f.

+Ví dụ 1 :   Cho mạch điện như hình vẽ. 

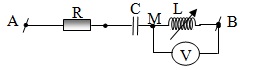
Điện áp giữa hai đầu AB có biểu thức \(u=200cos100\pi t(V)\) (V). Cuộn dây thuần cảm có L thay đổi được, điện trở R = 100Ω,

 tụ điện có điện dung \(C=\frac{10^{-4}}{\pi }(F)\). Xác định L sao cho điện áp

hiệu dụng giữa hai điểm M và B đạt giá trị cực đại, tính hệ số công suất của mạch điện khi đó.

Bài giải: Dung kháng:  \(Z_{C}=\frac{1}{\omega C}=\frac{1}{100\pi .\frac{10^{-4}}{\pi }}=100\Omega\)

Cách 1: Phương pháp đạo hàm

Cách 2: Phương pháp dùng tam thức bậc hai

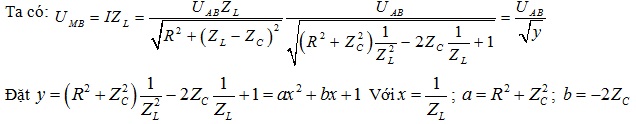
U_MBmax khi y_min:  Vì \(a=R^{2}+{Z_{C}}^{2}\)> 0 nên tam thức bậc hai đạt cực tiểu khi  \(x=-\frac{b}{2a}\)

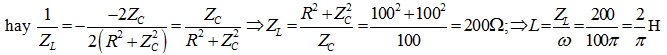
Hệ số công suất: \(cos\varphi =\frac{R}{\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}}=\frac{100}{\sqrt{100^{2}+(200-100)^{2}}}=\frac{\sqrt{2}}{2}\)

4.Sử dụng phương pháp cực trị của hàm số:

Về hàm số bậc 2: \(y=f(x)=ax^{2}+bx+c(a \neq 0)\)

+ Giá trị của x làm cho y cực trị là ứng với tọa độ đỉnh: \(x_{s}=x_{CT}=-\frac{b}{2a}(1)\)

+ 2 giá trị của \(x_{1};x_{2}\)  cho cùng một giá trị của hàm y, theo Viet:  \(x_{1}+x_{2}=-\frac{b}{a}(2)\)

            Từ (1) và (2) suy ra mối liên hệ: \(x_{CT}=\frac{1}{2}(x_{1}+x_{2})\)

      Về hàm phân thức:\(y=f(x)=ax+\frac{b}{x}\)

+ Giá trị của x làm y cực trị ứng với \(ax=\frac{b}{x}\Rightarrow x_{CT}=\sqrt{\frac{b}{a}}(3)\)

+ 2 giá trị của \(x_{1};x_{2}\)  cho cùng một giá trị của hàm y, theo Viet: \(x_{1}.x_{2}=\frac{b}{a}(4)\)

            Từ (3) và (4) suy ra mối liên hệ: \(x_{CT}=\sqrt{x_{1}x_{2}}\)

(Với những bài tập về cực trị của dòng điện xoay chiều, nếu ta sử dụng phương pháp này  thì sẽ có ngay đáp số, việc này rất thuận lợi cho học sinh làm rất nhanh những bài tập trắc nghiệm trong các kỳ thi ĐH-CĐ).

CÁC CÔNG THỨC  CỰC TRỊ TRONG ĐIỆN XOAY CHIỀU

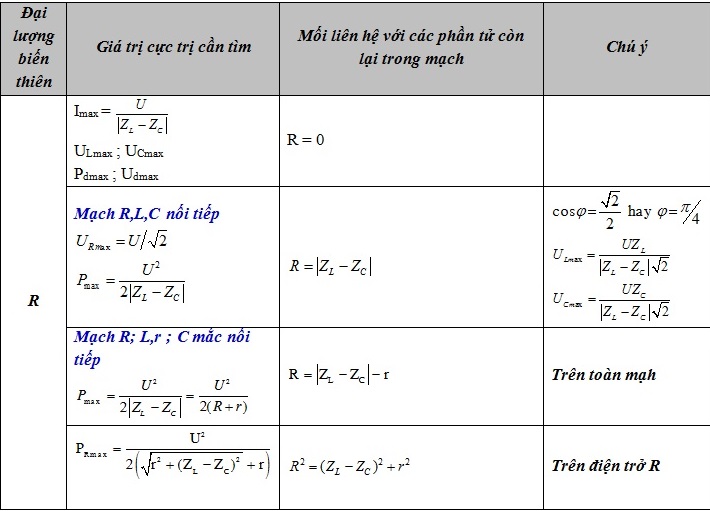
 a.Thay đổi R:

Câu 1: Cho đoạn mạch RLC mắc nối tiếp, R thay đổi được, cuộn dây không thuần cảm, có điện trở r. Khi R₁=20 Ω hoặc  R₂=110Ω  thì công suất trong mạch như nhau. Khi  R=50Ω thì công suất mạch cực đại. Điện trở thuần r của cuộn dây là bao nhiêu?

Giải Cách 1: làm theo kiểu tự luận cổ điển ( Các em tự giải nhé).

Cách 2: Sử dụng pp cực trị của hàm số .

Công suất mạch

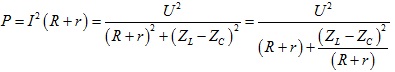
Ta  thấy có dạng phân thức với (R+r) nên ta sử dụng pp cực trị của hàm số .