Viết biểu thức của u hoặc i

VIẾT BIỂU THỨC CỦA u HOẶC i 

I.ĐOẠN MẠCH CHỈ CÓ 1 PHẦN TỬ:

  a) Đoạn mạch chỉ có điện trở thuần:

u_R cùng pha với i : I = \(\frac{U_{R}}{R}\)

  b) Đoạn mạch chỉ có tụ điện C:

u_C trễ pha so với i góc \(\frac{\pi }{2}\).

      - ĐL ôm:  I  = \(\frac{U_{C}}{Z_{C}}\) ; với Z_C = \(\frac{1}{\omega C}\) là dung kháng của tụ điện.

       -Đặt điện áp \(u=U\sqrt{2}cos\omega t\) vào hai đầu một tụ điện thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu tụ điện là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là :

          Ta có:\({\left( {{i \over {{I_0}}}} \right)^2} + {\left( {{u \over {{U_{0C}}}}} \right)^2} = 1 \Leftrightarrow {\rm{ }}{{{i^2}} \over {2{I^2}}}{\rm{ }} + {{{u^2}} \over {2{U_C}^2}} = 1 \Rightarrow {{{u^2}} \over {{U^2}}} + {{{i^2}} \over {{I^2}}} = 2\)

      -Cường độ dòng điện tức thời qua tụ: \(i=I\sqrt{2}cos(\omega t+\frac{\pi }{2})\)

  c) Đoạn mạch chỉ có cuộn dây thuần cảm L:

    u_L sớm pha hơn i góc \(\frac{\pi }{2}\) .

    - ĐL ôm:  I = \(\frac{U_{L}}{Z_{L}}\); với Z_L = ωL là cảm kháng của cuộn dây.

     -Đặt điện áp \(u=U\sqrt{2}cos\omega t\) vào hai đầu một cuộn cảm thuần thì cường độ dòng điện qua nó có giá

      trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu cuộn cảm thuần  là u và cường độ dòng điện

      qua nó là i. Hệ thức liên hệ giữa các đại lượng là :

           Ta có:  \({\left( {{i \over {{I_0}}}} \right)^2} + {\left( {{u \over {{U_{0L}}}}} \right)^2} = 1 \Leftrightarrow {{{i^2}} \over {2{I^2}}}{\rm{ }} + {{{u^2}} \over {2{U_L}^2}} = 1 \Rightarrow {{{u^2}} \over {{U^2}}} + {{{i^2}} \over {{I^2}}} = 2\)

        -Cường độ dòng điện tức thời qua cuộn dây:\(i=I\sqrt{2}cos(\omega t-\frac{\pi }{2})\)

d) Đoạn mạch có R, L, C không phân nhánh:

     +Đặt điện áp \(u=U\sqrt{2}cos(\omega t +\varphi _{u})\) vào hai đầu mạch

    + Độ lệch pha φ giữa u và i xác định theo biểu thức: 

\(tan\varphi =\frac{Z_{L}-Z_{C}}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}\); Với \(\varphi =\varphi _{u}-\varphi _{i}\)

     + Cường độ hiệu dụng xác định theo định luật Ôm: I = \(\frac{U}{Z}\).

        Với Z = \(\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}\)  là tổng trở của đoạn mạch.

         Cường độ dòng điện tức thời qua mạch:  \(i=I\sqrt{2}cos(\omega t+\varphi _{i})=I\sqrt{2}cos(\omega t+\varphi _{u}-\varphi )\)

     + Cộng hưởng điện trong đoạn mạch RLC:  Khi Z_L = Z_C hay \(\omega =\frac{1}{\sqrt{LC}}\)   thì

             I_max = \(\frac{U}{R},P_{max}=\frac{U^{2}}{R}\) ,   P_max = , u cùng pha với i (φ = 0).

Khi Z_L > Z_C  thì u nhanh pha hơn i (đoạn mạch có tính cảm kháng).

Khi Z_L < Z_C  thì u trể pha hơn i (đoạn mạch có tính dung kháng).

R tiêu thụ năng lượng dưới dạng toả nhiệt, Z_L và Z_C không tiêu thụ năng lượng điện.

 e) Đoạn mạch có R, L,r, C không phân nhánh:

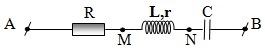
 +Đặt điện áp \(u=U\sqrt{2}cos(\omega t +\varphi _{u})\) vào hai đầu mạch

    + Độ lệch pha φ giữa u và i xác định theo biểu thức: 

\(tan\varphi =\frac{Z_{L}-Z_{C}}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}\); Với \(\varphi =\varphi _{u}-\varphi _{i}\)

     + Cường độ hiệu dụng xác định theo định luật Ôm: I = \(\frac{U}{Z}\).

        Với Z = \(\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}\)  là tổng trở của đoạn mạch.

         Cường độ dòng điện tức thời qua mạch:  \(i=I\sqrt{2}cos(\omega t+\varphi _{i})=I\sqrt{2}cos(\omega t+\varphi _{u}-\varphi )\)

+ Cách nhận biết cuộn dây có điện trở thuần r

-Xét toàn mạch, nếu: \(Z\neq \sqrt{R^{2}+(Z_{L}-Z_{C})^{2}};U\neq \sqrt{U_{R}^{2}+(U_{L}-U_{C})^{2}}\)

hoặc P  ≠ I²R hoặc cosφ ≠ \(\frac{R}{Z}\)        

   à thì cuộn dây có điện trở thuần r  ≠ 0.

-Xét cuộn dây, nếu: Ud  ≠  U_L hoặc Z_d  ≠ Z_L hoặc P_d   ≠ 0 hoặc cosφ_d  ≠ 0 hoặc φ_d  ≠ \(\frac{\pi }{2}\)  

  =>  thì cuộn dây có điện trở thuần r ≠ 0.

II.  PHƯƠNG PHÁP 1: (PHƯƠNG PHÁP TRUYỀN THỐNG):

a) Mạch điện chỉ chứa  một phần tử ( hoặc R, hoặc L, hoặc C)

- Mạch điện chỉ có điện trở thuần: u và i cùng pha: φ =φ_u - φ_i = 0 Hay  φ_u = φ_i

+ Ta có: \(i=I\sqrt{2}cos(\omega t+\varphi _{i})\)   thì  \(u=U_{R}\sqrt{2}cos(\omega t+\varphi )\)   ;  với \(I=\frac{U_{R}}{R}\).

   +Ví dụ 1: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có điện trở thuần R= 100Ω  có biểu thức u= \(200\sqrt{2}cos(100\pi t+\frac{\pi }{4})(V)\). Biểu thức của cường độ dòng điện trong mạch là : 

A. i=\(2\sqrt{2}cos(100\pi t-\frac{\pi }{4})(A)\)                               C.i=\(2\sqrt{2}cos(100\pi + \frac{\pi }{4})(A)\)

B. i=\(2\sqrt{2}cos(100\pi t+\frac{\pi }{2})(A)\)                                D.i=\(2cos(100\pi t-\frac{\pi }{2})(A)\)

   +Giải :Tính I₀ hoặc I= U /.R  =200/100 =2A; i cùng pha  với u hai đầu R, nên ta có:φ_i = φ_u = π/4

               Suy ra:  i =  \(2\sqrt{2}cos(100\pi + \frac{\pi }{4})(A)\)                                                             

=> Chọn C

 -Mạch điện chỉ có tụ điện: 

     u_C trễ pha so với i góc \(\frac{\pi }{2}\) . ->  φ= φ_u - φ_i =- \(\frac{\pi }{2}\)  Hay  φ_u = φ_i - \(\frac{\pi }{2}\) ; φ_i = φ_u +\(\frac{\pi }{2}\)

     +Nếu đề cho \(i=I\sqrt{2}cos(\omega t)\) thì viết: \(u=U\sqrt{2}cos(100\pi t-\frac{\pi }{2})(A)\) và ĐL Ôm:\(I=\frac{U_{C}}{Z_{C}}\)  với      \(Z_{C}=\frac{1}{\omega C}\)       

     +Nếu đề cho \(u=U\sqrt{2}cos(\omega t)\)  thì viết: \(i=I\sqrt{2}cos(100\pi t+\frac{\pi }{2})(A)\)

+Ví dụ 2:   Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có tụ có điện dung C= \(\frac{10^{-4}}{\pi }(F)\) có biểu thức u=\(200\sqrt{2}cos(100\pi t)(V)\). Biểu thức của cường độ dòng điện trong mạch là :

A. i=  \(2\sqrt{2}cos(100\pi t+\frac{5\pi }{6})(A)\)                         C.i=\(2\sqrt{2}cos(100\pi t+\frac{\pi }{2})(A)\)

B. i= \(2\sqrt{2}cos(100\pi t-\frac{\pi }{2})(A)\)                            D.i=\(2cos(100\pi t-\frac{\pi }{6})(A)\)

      Giải :  Tính  \(Z_{C}=\frac{1}{\omega C}=100\Omega\)  ,   Tính I_o hoặc I= U /.Z_L  =200/100 =2A;

    i sớm pha góc π/2 so với u hai đầu tụ điện;  Suy ra:  i=\(2\sqrt{2}cos(100\pi t+\frac{\pi }{2})(A)\) 

=> Chọn C

-Mạch điện chỉ có cuộn cảm thuần:

     u_L sớm pha hơn i góc  \(\frac{\pi }{2}\) . ->  φ= φ_u - φ_i =- \(\frac{\pi }{2}\)  Hay  φ_u = φ_i + \(\frac{\pi }{2}\) ; φ_i = φ_u - \(\frac{\pi }{2}\)

    +Nếu đề cho  \(i=I\sqrt{2}cos(\omega t)\)  thì viết: \(u=U\sqrt{2}cos(100\pi t+\frac{\pi }{2})(A)\)  và ĐL Ôm: \(I=\frac{U_{L}}{Z_{L}}\) với   \(Z_{L}=\omega L\)                      

      Nếu đề cho \(u=U\sqrt{2}cos(\omega t)\) thì viết: \(i=I\sqrt{2}cos(100\pi t-\frac{\pi }{2})(A)\)

 Ví dụ 3:  Hiệu điện thế giữa hai đầu một đoạn mạch điện xoay chiều chỉ có cuộn cảm có độ tự cảm  L= \(\frac{1}{\pi }(H)\) có biểu thức u=\(200\sqrt{2}cos(100\pi t+\frac{\pi }{3})(V)\). Biểu thức cường độ dòng điện trong mạch là :

A. i=   \(2\sqrt{2}cos(100\pi t+\frac{5\pi }{6})(A)\)                        C.i=\(2\sqrt{2}cos(100\pi t-\frac{\pi }{6})(A)\)

B. i=\(2\sqrt{2}cos(100\pi t+\frac{\pi }{6})(A)\)                              D.i=\(2cos(100\pi t-\frac{\pi }{6})(A)\)

Giải :  Tính   \(Z_{L}=\omega L\)  = 100π.1/π =100Ω,  Tính I₀ hoặc I= U /.Z_L  =200/100 =2A;

           i trễ pha góc π/2 so với u hai đầu cuộn cảm thuần, nên ta có: \(\frac{\pi }{3}-\frac{\pi }{2}=-\frac{\pi }{6}\)

           Suy ra:  i = \(2\sqrt{2}cos(100\pi t-\frac{\pi }{6})(A)\)

=> Chọn C

II.MẠCH ĐIỆN KHÔNG PHÂN NHÁNH (R L C)

a. Phương pháp truyền thống):

-Phương pháp giải:    Tìm Z, I ( hoặc I₀ )và φ 

 Bước 1:  Tính tổng trở Z: Tính \(Z_{L}=\omega L\) ; \(Z_{C}=\frac{1}{\omega C}=\frac{1}{2\pi fC}\)  và  \(Z=\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}\)

Bước 2:   Định luật Ôm : U và I liên hệ với nhau bởi ; I= \(\frac{U}{Z}\) I_o = \(\frac{U_{0}}{Z}\);

 Bước 3:  Tính độ lệch  pha giữa u hai đầu mạch và i: \(tan\varphi =\frac{Z_{L}-Z_{C}}{R}\); 

 Bước 4:  Viết biểu thức u hoặc i

  -Nếu cho trước:\(i=I\sqrt{2}cos(\omega t)\)  thì biểu thức của  u là   \(u=U\sqrt{2}cos(\omega t+\varphi )\)

                     Hay i = I_ocosωt                                         thì u = U_ocos(ωt + φ).                

  -Nếu cho trước: \(u=U\sqrt{2}cos(\omega t)\) thì biểu thức của  i  là: \(i=I\sqrt{2}cos(\omega t-\varphi )\)

                 Hay u = U_ocosωt                                        thì  i = I_ocos(ωt - φ)

    * Khi: (φu ≠ 0;  φ i ≠ 0 ) Ta có :  φ = φu - φ i  => φu = φi + φ  ; φi = φu - φ  

  -Nếu cho trước \(i=I\sqrt{2}cos(\omega t+\varphi_{i} )\)  thì biểu thức của u là:  \(u=U\sqrt{2}cos(\omega t+\varphi_{i} +\varphi )\)

                    Hay i = I_ocos(ωt + φi)                                       thì u = U_ocos(ωt + φi + φ).         

  -Nếu cho trước \(u=U\sqrt{2}cos(\omega t+\varphi_{u} )\)thì biểu thức của i là: \(i=I\sqrt{2}cos(\omega t+\varphi_{u}-\varphi )\)

                Hay u = U_ocos(ωt +φu)                                       thì  i = I_ocos(ωt +φu - φ)

Lưu ý: Với Mạch điện không phân nhánh có cuộn dây không cảm thuần (R ,L,r, C) thì:

Tổng trở :\(Z=\sqrt{(R+r)^{2}+(Z_{L}-Z_{C})^{2}}\)   và \(tan\varphi =\frac{Z_{L}-Z_{C}}{R+r}\);  

Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm \(L=\frac{1}{\pi }(H)\) và một tụ điện có điện dung \(C=\frac{2.10^{-4}}{\pi }(F)\)  mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng \(i=5cos100\pi t(A)\) .Viết biểu thức điện áp tức thời giữa hai đầu  mạch điện.

Giải :

 Bước 1: Cảm kháng: \(Z_{L}=\omega L=100\pi .\frac{1}{\pi }=100\Omega ;\); Dung kháng: \(Z_{C}=\frac{1}{\omega C}=\frac{1}{100\pi .\frac{2.10^{-4}}{\pi }}=50\Omega\)

         Tổng trở:  \(Z=\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}=\sqrt{50^{2}+(100-50)^{2}}=50\sqrt{2}\Omega\)

Bước 2:  Định luật Ôm :  Với U_o= I_oZ = 5.50\(\sqrt{2}\) = 250\(\sqrt{2}\)V;       

Bước 3:  Tính độ lệch  pha giữa u hai đầu mạch và i:  \(tan\varphi =\frac{Z_{L}-Z_{C}}{R}=\frac{100-50}{50}=1\Rightarrow \varphi =\frac{\pi }{4}\)(rad).

Bước 4:   Biểu thức điện áp tức thời giữa hai đầu mạch điện: \(u=250\sqrt{2}cos(100\pi t+\frac{\pi }{4})(V)\)(V).

b.PHƯƠNG PHÁP  DÙNG SỐ PHỨC TÌM BIỂU THỨC i HOẶC u

VỚI MÁY CASIO FX-570ES; FX-570ES PLUS;VINACAL-570ES PLUS .

 (NHANH VÀ HIỆU QUẢ CHO TRẮC NGHIỆM)

1.Tìm hiểu các đại lượng xoay chiều dạng phức: Xem bảng liên hệ 

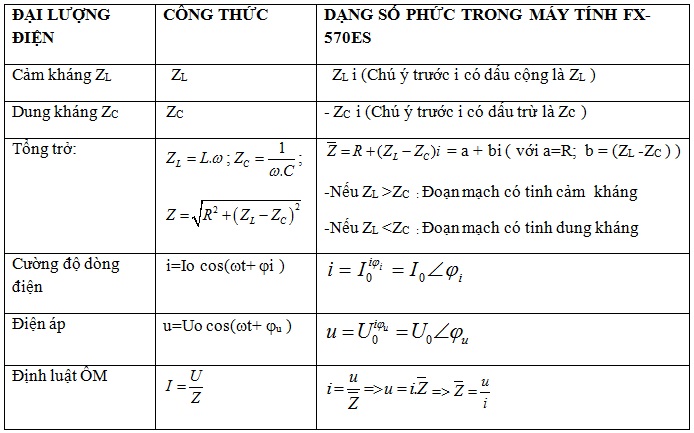
Chú ý: \(\bar{Z}=R+(Z_{L}-Z_{C})i\)( tổng trở phức \(\bar{Z}\) có gạch trên đầu: R là phần thực, (Z_L -Z_C ) là phần ảo)

            Cần phân biệt chữ i sau giá trị b = (Z_L -Z_C )  là phần ảo , khác với  chữ i  là cường độ dòng điện

2.Chọn cài dặt  máy tính: CASIO fx – 570ES ; 570ES Plus

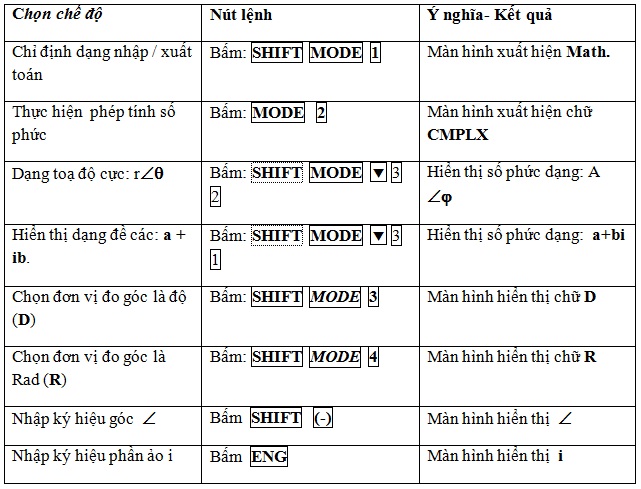
3.Lưu ý Chế độ hiển thị kết quả trên màn hình:

Sau khi nhập, ấn dấu =  có thể hiển thị kết quả dưới dạng số vô tỉ,

muốn kết quả dưới dạng thập phân ta  ấn SHIFT  =  

( hoặc nhấn phím S<=>D  ) để chuyển đổi kết quả Hiển thị.

4. Các Ví dụ 1:

Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm \(L=\frac{1}{\pi }(H)\) và một tụ điện có điện dung \(C=\frac{2.10^{-4}}{\pi }(F)\)  mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng \(i=5cos100\pi t(A)\) .Viết biểu thức điện áp tức thời giữa hai đầu  mạch điện.

Giải :  \(Z_{L}=\omega L=100\pi .\frac{1}{\pi }=100\Omega ;Z_{C}=\frac{1}{\omega C}=...=50\Omega\)   Và Z_L-Z_C =50Ω

-Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện: CMPLX.

 -Bấm  SHIFT MODE  ‚ 3 2 :  dạng hiển thị toạ độ cực:( r\(\angle\)\(\Theta\) )

 -Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3   màn hình hiển thị  D

  Ta có :\(u=i.\bar{Z}=I_{0}\angle \varphi _{i}X(R+(Z_{L}-Z_{C}))i=5\angle 0X(50+50i)\)      ( Phép NHÂN hai số phức)

  Nhập máy: 5 SHIFT (-)  0   X   ( 50  +  50   ENG i ) =  Hiển thị: 353.55339\(\angle\)45 = 250\(\sqrt{2}\)\(\angle\)45

 Vậy biểu thức tức thời điện áp của  hai đầu mạch:

 u = 250\(\sqrt{2}\) cos( 100πt +π/4) (V).

Ví dụ 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100Ω; \(C=\frac{1}{\pi }.10^{-4}F;L=\frac{2}{\pi }H\). Cường độ dòng điện qua mạch có dạng: i = 2\(\sqrt{2}\)cos100πt(A). Viết biểu thức điện áp tức thời của hai đầu mạch?

  Giải: . \(Z_{L}=\omega L=100\pi .\frac{2}{\pi }=200\Omega ;Z_{C}=\frac{1}{\omega C}=...=100\Omega\)Và Z_L-Z_C =100Ω

 -Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.

 -Bấm  SHIFT MODE  ‚ 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )

 -Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3  màn hình hiển thị D

  Ta có : \(u=i.\bar{Z}=I_{0}\angle \varphi _{i}X(R+(Z_{L}-Z_{C}))i=2\sqrt{2}\angle 0X(100+100i)\)     ( Phép NHÂN hai số phức)

  Nhập máy: 2\(\sqrt{2}\) \(\triangleright\) SHIFT (-)  0   X   (  100    +  100   ENG i ) =  Hiển thị: 400\(\angle\)45

 Vậy biểu thức tức thời điện áp của  hai đầu mạch: u = 400cos( 100πt +π/4) (V).

Ví dụ 3: Cho đoạn mạch xoay chiều có R=40Ω, \(L=\frac{1}{\pi }(H),C=\frac{10^{-4}}{0,6\pi }(F)\), mắc nối tiếp  điện áp 2 đầu mạch  u=100\(\sqrt{2}\)cos100πt (V), Cường độ dòng điện qua mạch là:

      A.\(i=2,5cos(100\pi t+\frac{\pi }{4})(A)\)                                 B.\(i=2,5cos(100\pi t-\frac{\pi }{4})(A)\)

      C.\(i=2cos(100\pi t-\frac{\pi }{4})(A)\)                                      C.\(i=2cos(100\pi t+\frac{\pi }{4})(A)\)

  Giải: \(Z_{L}=\omega L=100\pi .\frac{1}{\pi }=100\Omega ;Z_{C}=\frac{1}{\omega C}=\frac{1}{100\pi .\frac{10^{-4}}{0,6\pi }}=60\Omega\). Và Z_L-Z_C =40Ω

  -Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện: CMPLX.

   -Bấm  SHIFT MODE  ‚ 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\)  )

 -Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3   màn hình hiển thị D

  Ta có : \(i=\frac{u}{\bar{Z}}=\frac{U_{0}\angle \varphi _{u}}{(R+(Z_{L}-Z_{C}))i}=\frac{100\sqrt{2}\angle 0}{(40+40i)}\)    ( Phép CHIA hai số phức)

  Nhập 100\(\sqrt{2}\) \(\triangleright\) SHIFT (-)  0   :   (  40    +  40   ENG i ) =  Hiển thị: 2,5\(\angle\)-45

 Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:

i = 2,5cos(100πt -π/4) (A).

 Chọn B

Ví dụ 4:  Một đoạn mạch điện gồm điện trở R = 50Ω mắc nối tiếp với cuộn thuần cảm L = 0,5/π (H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = 100\(\sqrt{2}\)cos(100πt- π/4) (V). Biểu thức của cường độ dòng điện qua đoạn mạch là:

        A. i  = 2cos(100πt- π/2)(A).                                        B. i  = 2\(\sqrt{2}\)cos(100πt- π/4) (A).

        C. i  = 2\(\sqrt{2}\)cos100πt (A).                                            D. i  = 2cos100πt (A).

Giải:  \(Z_{L}=\omega L=100\pi .\frac{0,5}{\pi }=50\Omega\) Và Z_L-Z_C =50Ω - 0 = 50Ω

  -Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện: CMPLX.

 -Bấm  SHIFT MODE  ‚ 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )

 -Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3   màn hình hiển thị  D

  Ta có : \(i=\frac{u}{\bar{Z}}=\frac{U_{0}\angle \varphi _{u}}{(R+Z_{L}i}=\frac{100\sqrt{2}\angle -45}{(50+50i)}\)   ( Phép CHIA hai số phức)

  Nhập 100\(\sqrt{2}\) \(\triangleright\) SHIFT (-)  - 45   :   (  50    +  50   ENG i ) =  Hiển thị: 2\(\angle\)- 90

 Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:

i = 2cos( 100πt - π/2) (A). 

Chọn A

Ví dụ 5(ĐH 2009):  Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm L = 1/4π (H) thì cường độ dòng điện 1 chiều là 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp u =150\(\sqrt{2}\)cos120πt (V) thì biểu thức cường độ dòng điện trong mạch là:

  A.\(i=5\sqrt{2}cos(120\pi t-\frac{\pi }{4})(A)\)                       B.  \(i=5cos(120\pi t+\frac{\pi }{4})(A)\)

  C.\(i=5\sqrt{2}cos(120\pi t+\frac{\pi }{4})(A)\)                       D.\(i=5cos(120\pi t-\frac{\pi }{4})(A)\)

  Giải:  Khi đặt hiệu điện thế không đổi (hiệu điện thế 1 chiều) thì đoạn mạch chỉ còn có R: R = U/I =30Ω

    \(Z_{L}=\omega L=120\pi .\frac{1}{4\pi }=30\Omega;i=\frac{u}{\bar{Z}}=\frac{150\sqrt{2}\angle 0}{(30+30i)}\)   ( Phép CHIA hai số phức)

 a.Với máy FX570ES :

-Bấm MODE 2 màn hình xuất hiện: CMPLX.

-Bấm  SHIFT MODE  ‚ 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )

-Chọn đơn vị góc là độ (D), bấm: SHIFT MODE 3  màn hình hiển thị D

  Nhập máy: 150\(\sqrt{2}\) \(\triangleright\) :   (  30   +  30   ENG i ) =  Hiển thị: 5\(\angle\)- 45

 Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là: 

i = 5cos( 120πt - π/4) (A). 

Chọn D

b.Với máy FX570ES : -Bấm MODE 2 màn hình xuất hiện: CMPLX.

-Chọn đơn vị  góc là độ (R), bấm: SHIFT MODE 4  màn hình hiển thị R

Nhập máy: 150 \(\sqrt{2}\) \(\triangleright\) :   (  30    +  30   ENG i ) =  Hiển thị dạng phức: 3.535533..-3.535533…i

  Bấm  SHIFT 2 3 : Hiển thị: 5\(\angle\) - \(\frac{\pi }{4}\)

 Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là:

 i = 5cos( 120πt - π/4) (A). 

Chọn D