Bài toán ngược xác định RLC

BÀI TOÁN NGƯỢC XÁC ĐỊNH RLC

Tính tổng trở Z, điện trở R - cảm kháng Z_L – dung kháng Z_C – độ tự cảm L và điện dung C

1.Phương pháp chung:

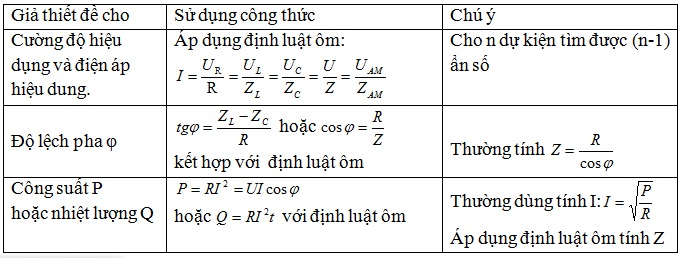
+Nhớ các công thức về ĐL Ôm, công thức tính tổng trở....:

-   Biết U và I: Z=U/I

-   Biết Z_L, Z_C và R: \(Z=\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}\) :\(Z_{L}=\omega L,Z_{C}=\frac{1}{\omega C}\)  , với L có đơn vị (H) và C có đơn vị (F)

-   Biết R và j hoặc cosj : Z=R/cosφ

Nếu cuộn cảm có điện trở hoạt động r thì mạch RLrC sẽ có điện trở thuần tương đương là R+ r; khi đó \(Z=\sqrt{(r+R)^{2}+(Z_{L}-Z_{C})^{2}}\)

+Công thức tính điện trở  R:

-   Nếu biết L, C và φ: tính theo: \(tan\varphi =\frac{Z_{L}-Z_{C}}{R}\) ; Nếu cuộn cảm có điện trở r: \(tan\varphi =\frac{Z_{L}-Z_{C}}{r+R}\)

-   Biết Z và φ hoặc cosφ : R= Z.cosφ;     Nếu cuộn cảm có điện trở r:\(cos\varphi =\frac{r+R}{Z}\)

-   Biết P và I:\(P=RI^{2}\) ;  Nếu cuộn cảm có điện trở r: Công suất toàn mạch : P= (r+R)I²

+Công thức tính cảm kháng Z_L và dung kháng Zc:  \(Z_{L}=\omega L=2\pi fL;Z_{C}=\frac{1}{\omega C}=\frac{1}{2\pi fC}\)  ; 

-  Biết Z và R, tính được hiệu:\((Z_{L}-Z_{C})=\pm \sqrt{Z^{2}-R^{2}}\)sau đó tính được Z_L nếu biết Zc và ngược lại, từ đó tính L và C

-Chú ý thêm : \(Z_{L}.Z_{C}=\frac{L}{C}\) ; cộng hưởng điện : Z_L= Z_C hay :\(\omega ^{2}LC=1\)  hay\(\omega =\frac{1}{\sqrt{LC}}\)

-Khi bài toán cho các điện áp hiệu dụng thành phần và hai đầu mạch, cho công suất tiêu thụ nhưng chưa cho dòng điện thì hãy lập phương trình với điện áp hiệu dụng.

-Khi tìm ra U_R sẽ tìm \(I=\frac{P}{U_{R}}\) sau đó tìm \(R=\frac{U_{R}}{I};Z_{L}=\frac{U_{L}}{I};Z_{C}=\frac{U_{C}}{I}\)

-Công suất thiêu thụ : \(P=U.I.cos\varphi =I^{2}R=\frac{U^{2}R}{Z^{2}}\)   ; Hay  \(P=\frac{U^{2}R}{R^{2}+(Z_{L}-Z_{C})^{2}}\) hay  P= U_RI

- Hệ số công suất  \(k=cos\varphi =\frac{R}{Z}=\frac{P}{UI}=\frac{U_{R}}{U}\)

- Nhiệt lượng toả ra trên mạch ( chính là trên R): Q = RI²t ( t có đơn vị: s, Q có đơn vị: J)

-Cũng cần phải nghĩ đến giản đồ véc tơ vẽ  mạch điện đó để bảo đảm hệ phương trình không bị sai.

2. Các Ví dụ 1:

+ Ví dụ 1: Tính tổng trở của các mạch điện sau:

a. Cho mạch RLC không phân nhánh: U_C = 4V; U_R =16V; U_L=20V; I=2A

b. Cho Mạch RL nối tiếp có R=20Ω; u lệch pha 60^o so với i

c. Cho Mạch RC nối tiếp có R=10Ω; u lệch pha 30^o so với i

d Cho Mạch RLC nối tiếp có R=60Ω; hệ số công suất 0,6

Giải:

a.Vì đề cho I và các U_C;U_R,U_L nên ta dùng các công thức :

R = U_R/I = 16/2 = 8 Ω; Z_L= U_L/I = 20/2=10Ω ; Z_C= U_C/I = 4/2=2Ω ;

Suy ra:  Z=  \(\sqrt{8^{2}+(10-2)^{2}}=8\sqrt{2}\Omega\)

b.Vì đề cho: R = 20 Ω; φ = \(\frac{\pi }{3}\)  nên ta có: tan φ = \(\frac{Z_{L}}{R}\) => Z_L = R. tan φ =20\(\sqrt{3}\) Ω.

c. Vì đề cho: R = 10 Ω; φ =\(-\frac{\pi }{6}\) nên ta có: tan φ = \(-\frac{Z_{C}}{R}\) => Z_C = -R. tan φ=10\(\frac{\sqrt{3}}{3}\) Ω.

d. Vì đề cho: R = 60 Ω;  cosφ =0,6  mà cosφ =\(\frac{R}{Z}\) => Z =\(\frac{R}{cos\varphi }\)  = 60/ 0,6 = 100 Ω.

+ Ví dụ 2:  Cho mạch điện xoay chiều như hình vẽ. U_AB=const; f=50(Hz) , điện trở các khóa K và ampe kế không đáng kể. \(C=\frac{10^{-4}}{\pi }(F)\). Khi khóa K chuyển từ vị trí 1 sang 2 thì số chỉ của ampe kế không thay đổi. Tính độ tự cảm L của cuộn dây ?

A. \(\frac{10^{-2}}{\pi }(H)\)              B.\(\frac{10^{-1}}{\pi }(H)\)                  C. \(\frac{1}{\pi }(H)\)                 D.\(\frac{10}{\pi }(H)\)

Giải: \(Z_{C}=100\Omega ;\omega =100\pi (rad/s)\)

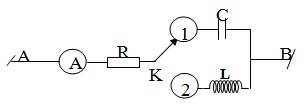
Khi khóa K ở vị trí 1 mạch là hai phần tử R và C.

Nên ta có :\(I=\frac{U_{AB}}{Z_{AB}}=\frac{U_{AB}}{\sqrt{R^{2}+{Z_{C}}^{2}}}(1)\)

Khi khóa K ở vị trí 2 thì mạch bao gồm hai phần tử là R và L:

Nên ta có :  \(I'=\frac{U_{AB}}{Z'_{AB}}=\frac{U_{AB}}{\sqrt{R^{2}+{Z_{L}}^{2}}}(2)\)

Theo đề I=I’ nên  (1) = (2) :\(\frac{U_{AB}}{\sqrt{R^{2}+{Z_{C}}^{2}}}=\frac{U_{AB}}{\sqrt{R^{2}+{Z_{L}}^{2}}}\)

Suy ra:  \(\frac{1}{\sqrt{R^{2}+{Z_{C}}^{2}}}=\frac{1}{\sqrt{R^{2}+{Z_{L}}^{2}}}\rightarrow \sqrt{R^{2}+{Z_{C}}^{2}}=\sqrt{R^{2}+{Z_{L}}^{2}}\)

\(\rightarrow Z_{L}=Z_{C}=100\Omega \Rightarrow L=\frac{Z_{L}}{\omega }=\frac{100}{100\pi }=\frac{1}{\pi }(H)\)

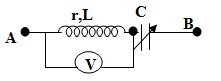
+Ví dụ 3 : Cho mạch điện như hình vẽ: u= \(120\sqrt{2}cos(100\pi t)\)(V); cuộn dây có r =15Ω; \(L=\frac{2}{25\pi }(H)\). C là tụ điện biến đổi. Điện trở vôn kế lớn vô cùng. Điều chỉnh C để số chỉ vôn kế lớn nhất. Tìm C và số chỉ vôn kế lúc này?

A.\(C=\frac{10^{-2}}{8\pi }(F);U_{V}=136(V)\)        B.\(C=\frac{10^{-2}}{4\pi }(F);U_{V}=163(V)\)

C.\(C=\frac{10^{-2}}{3\pi }(F);U_{V}=136(V)\)          D.\(C=\frac{10^{-2}}{5\pi }(F);U_{V}=186(V)\)

Giải: Do vôn kế mắc vào hai đầu cuộn dây nên số chỉ vôn kế là : 

\(U_{V}=U_{d}=I.Z_{d}=\frac{U}{Z}.Z_{d}=\frac{U}{\sqrt{r^{2}+(Z_{L}-Z_{C})^{2}}}.\sqrt{r^{2}+(\omega L)^{2}}\)

Do Z_d không phụ thuộc C nên nó không đổi. Vậy biểu thức trên tử số không đổi.

=> số chỉ Vôn kế lớn nhất khi mẫu số bé nhất:  \((\sqrt{r^{2}+(Z_{L}-Z_{C})^{2}})_{min}\)

Điều này xảy ra khi cộng hưởng điện: \(Z_{C}=Z_{L}=8(\Omega )\).

Suy ra : \(C=\frac{10^{-2}}{8\pi }(F)\) , Lúc đó Z = r

Và số chỉ vôn kế :\(U_{V}=U_{d}=\frac{U}{r}.\sqrt{r^{2}+(\omega L)^{2}}=\frac{120}{15}.\sqrt{15^{2}+(8)^{2}}=\frac{120}{15}.17=136V\)     

Chọn  A.

+Ví dụ 4 :  Mạch điện xoay chiều gồm một cuộn dây có điện trở r = 30W, độ tự cảm H mắc nối tiếp với tụ điện có điện dung C. Điện áp tức thời giữa hai đầu đoạn mạch là: (V). Với giá trị nào của C thì công suất tiêu thụ của mạch có giá trị cực đại và giá trị công suất cực đại bằng bao nhiêu?

          A. \(C=\frac{10^{-4}}{2\pi }\)F và \(P_{max}=120\)W.           B. \(C=\frac{10^{-4}}{\pi }\)F và \(P_{max}=120\sqrt{2}\)W.

          C. \(C=\frac{10^{-3}}{4\pi }\)F và \(P_{max}=240\)W.           D. \(C=\frac{10^{-3}}{\pi }\)F và \(P_{max}=240\sqrt{2}\)W.

Giải :  Công suất: \(P=I^{2}r=\frac{U^{2}r}{r^{2}+(Z_{L}-Z_{C})^{2}}\)    Ta có P_max <=> \(Z_{L}=Z_{C})^{2}\Leftrightarrow \frac{1}{\omega C}=\omega L\)

      \(C=\frac{1}{\omega^{2} L}=\frac{1}{(100\pi )^{2}.\frac{0,4}{\pi }}=\frac{10^{-3}}{4\pi }F\Rightarrow P_{max}=\frac{U^{2}}{r}=\frac{120^{2}}{2.30}=240W\)                  

Chọn  C.

+Ví dụ 5 :  Cho mạch điện không phân nhánh. R = 100Ω, cuộn dây có độ tự cảm L = 0,318 H, f = 50Hz, tụ điện có điện dung thay đổi. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng \(U=100\sqrt{2}\)V. Điều chỉnh C để mạch có cộng hưởng điện. Giá trị C và cường độ dòng điện khi đó là:

          A. C = 31,8mF và I= \(\sqrt{2}\)A.             B. C = 31,8mF và I=2\(\sqrt{2}\)A.

          C. C = 3,18mF và I= 3\(\sqrt{2}\) A.            D. C = 63,6mF và I = 2A.

Giải : Cảm kháng: \(Z^{L}=2\pi fL=2\pi .50.0,318=100\Omega\); Mạch có cộng hưởng khi Z_C = Z_L = 100Ω.

\(\Rightarrow C=\frac{1}{2\pi f.Z_{C}}=\frac{1}{2\pi .50.100}=\frac{10^{-4}}{\pi }F=31,8\mu F;\)\(I_{max}=\frac{U}{R}=\frac{100\sqrt{2}}{100}=\sqrt{2}A\)

Chọn  A.

+Ví dụ 6 :  Cho mạch điện gồm R, L, C nối tiếp. R thay đổi \(L=\frac{1}{\pi }H,C=\frac{10^{-3}}{4\pi }F\) Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u=75\sqrt{2}cos100\pi t(V)\). Công suất trên toàn mạch là P = 45W. Điện trở R có giá trị bằng bao nhiêu?

          A. R = 45Ω                   B. R = 60Ω                   C. R = 80Ω            D. câu A hoặc C

Giải : 

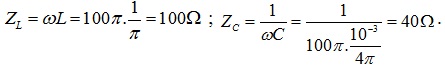
Công suất tiêu thụ:

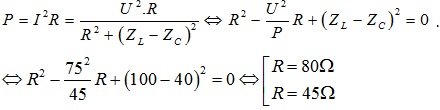
Chọn  D.

+Ví dụ 7 :   Cho đoạn mạch gồm điện trở thuần R = 100Ω và tụ điện có điện dung C mắc nối tiếp. Biết biểu thức hiệu điện thế giữa 2 đầu đoạn mạch u = 100 cos100πt V  và cường độ hiệu dụng trong mạch I= 0,5 A. Tính tổng trở của đoạn mạch và điện dung của tụ điện?

A. Z=100\(\sqrt{2}\)Ω ; C=\(\frac{1}{\omega Z_{C}}=\frac{1}{\pi }.10^{-4}F\)              B. . Z=200\(\sqrt{2}\)Ω ; C= \(\frac{1}{\omega Z_{C}}=\frac{1}{\pi }.10^{-4}F\)

C. Z=50\(\sqrt{2}\)Ω ; C=\(\frac{1}{\omega Z_{C}}=\frac{1}{\pi }.10^{-4}F\)                D. . Z=100\(\sqrt{2}\)Ω ; C= \(\frac{1}{\omega Z_{C}}=\frac{1}{\pi }.10^{-3}F\)

HD GIẢI:Chọn A. ĐL ôm Z= U/I =100\(\sqrt{2}\)Ω ;dùng công thức Z =\(Z=\sqrt{R^{2}+{Z_{C}}^{2}}=\sqrt{100^{2}+{Z_{C}}^{2}}\)

Suy ra \(Z_{C}=\sqrt{Z^{2}-R^{2}}=\sqrt{2.100^{2}-100^{2}}=100\Omega\) ;C=\(\frac{1}{\omega Z_{C}}=\frac{1}{\pi }.10^{-4}F\)

+Ví dụ 8:

Một mạch điện xoay chiều ABDEF gồm các linh kiện sau đây mắc nối tiếp (xem hình vẽ)

- Một cuộn dây cảm thuần có hệ số tự cảm L.

- Hai điện trở giống nhau, mỗi cái có giá trị R.

- Một tụ điện có điện dung C.

Đặt giữa hai đầu A, F của mạch điện một điện áp xoay chiều có giá trị hiệu dung U­_AF = 50V và có tần số f = 50Hz.. Điện áp giữa hai đầu các đoạn mạch AD và BE đo được là U_AD = 40V và U_BE = 30V.Cường độ dòng điện hiệu dụng trong mạch là I = 1A

a) Tính các giá trị R, L và C

b) Tính hệ số công suất của mạch điện

c) Tính độ lệch pha giữa các hiệu điện thế U_AD và U_DF.                         

ĐH Tài chính Kế toán - 1999

Giảia) Tổng trở 

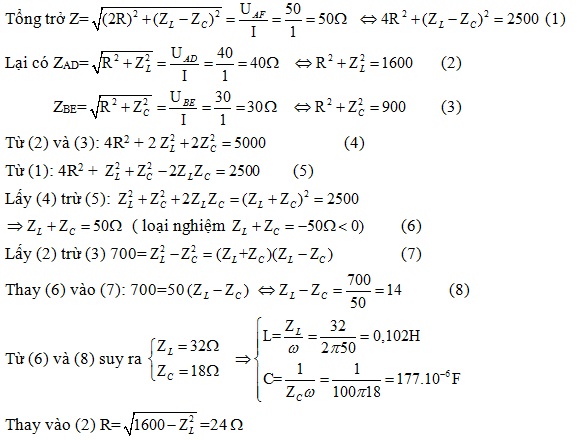
b) Hệ số công suất \(cos\varphi =\frac{2R}{Z}=\frac{2.24}{50}=0,96\)

    c) u_AD sớm pha hơn i là φ₁ với tanφ₁= \(-\frac{Z_{C}}{R}=\frac{3}{4}\); 

u_DF sớm pha hơn i là φ₂ với tanφ₂=\(\frac{Z_{L}}{R}=\frac{4}{3}\)

Ta có tanφ₁. tanφ₂= - 1 nghĩa là u_AD sớm pha hơn u_DF là \(\frac{\pi }{2}\) .

+Ví dụ 9:Mạch điện xoay chiều, gồm điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Đặt vào 2 đầu đoạn mạch một điện áp xoay chiều u tần số 1000Hz. Khi mắc 1 ampe kế A có điện trở không đáng kể song song với tụ C thì nó chỉ 0,1A. Dòng điện qua nó lệch pha so với điện áp hai đầu đoạn mạch góc  π/6 rad. Thay ampe kế A bằng vôn kế V có điện trở rất lớn thì vôn kế chỉ 20V, điện áp hai đầu vôn kế chậm pha hơn điện áp hai đầu đoạn mạch  π/6 rad. Độ tự cảm L và điện trở thuần  R có giá trị:

Giải: *Mắc ampe kế song song tụ,nên tụ bị nối tắt => mạch chỉ còn R, L. và I₁=0,1A
            -Độ lệch pha: φ₁ = π/6 => \(R=\sqrt{3}Z_{L}\) (1).
           -Ta có: \(U=I.Z=0,1.\sqrt{R^{2}+{Z_{L}}^{2}}=0,1.\sqrt{R^{2}+\frac{R^{2}}{3}}=0,1.\sqrt{\frac{4R^{2}}{3}}=0,2\frac{R}{\sqrt{3}}\)(2)
      *Mắc vôn kế vào C, Uc = 20V.mạch có R, L,C.
          -Ta có uc chậm pha hơn u /6 rad =>φ₂ = -π/3 => \(\sqrt{3}R=Z_{C}-Z_{L}\).

         \(\Rightarrow Z=2R\) . Do U mạch không đổi => \(I=\frac{U}{Z}=\frac{0,2R}{\sqrt{3}.2R}=\frac{0,1}{\sqrt{3}}\)
          -Ta có:\(Z_{C}=\frac{U_{C}}{I}=\frac{20}{\frac{0,1}{\sqrt{3}}}=200\sqrt{3}\Omega\)

           -Lấy (3) chia (1) và biến đổi ta có:\(Z_{L}=\frac{Z_{C}}{4}=\frac{200\sqrt{3}}{4}=50\sqrt{3}\Omega\)

        \(\Rightarrow Z_{L}=2\pi fL\Rightarrow L=\frac{Z_{L}}{2\pi f}=\frac{50\sqrt{3}}{200\pi }=\frac{\sqrt{3}}{40\pi }(H)\)
       -Từ (1) ta tìm được .\(R=\sqrt{3}Z_{L}=\sqrt{3}.50\sqrt{3}=150\Omega\)

ĐA: A

3. Trắc nghiệm:

Câu 1. Đoạn mạch xoay chiều gồm cuộn dây thuần cảm mắc nối tiếp với điện trở thuần. Điện áp hai đầu mạch sớm pha \(\frac{\pi }{3}\) so với dòng điện trong mạch và U = 160V, I = 2A; Giá trị của điện trở thuần là:

    A.80\(\sqrt{3}\) Ω                       B.80 Ω                      C.40\(\sqrt{3}\)Ω                    D. 40 Ω

Câu 2:  Một cuộn dây mắc vào nguồn xoay chiều u = 200cos(100π t- π/2) (V), thì cường độ dòng điện qua cuộn dây là: i = \(\sqrt{2}\) cos (100πt - \(\frac{5\pi }{6}\)). Hệ số tự cảm của cuộn dây là:

A. L = \(\frac{\sqrt{2}}{\pi }\) H                        B. L = \(\frac{1}{\pi }\) H                C. L = \(\frac{\sqrt{6}}{2\pi }\) H                 D. L =  \(\frac{2}{\pi }\) H

Câu 3. Cho mạch điện xoay chiều RLC không phân nhánh và một ampe kế đo cường độ dòng điện trong mạch. Cuộn dây có \(r=10\Omega ,L=\frac{1}{10\pi }H\), Đặt vào hai đầu đoạn mạch một điện áp dao động điều hoà có giá trị hiệu dụng là U = 50 V và tần số f = 50 Hz. Khi điện dung của tụ điện có giá trị là C₁ thì số chỉ của ampe kế là cực đại và bằng 1A. Giá trị của R và C₁ là
A. R=40Ω và \(C_{1}=\frac{10^{-3}}{\pi }F\)                                     B.R=50Ω  và \(C_{1}=\frac{2.10^{-3}}{\pi }F\)
C.  R=40Ω và  \(C_{1}=\frac{2.10^{-3}}{\pi }F\)                                D. R=50Ω và \(C_{1}=\frac{10^{-3}}{\pi }F\)

Câu 4. Cho một đoạn mạch điện xoay chiều AB gồm điện trở thuần R nối tiếp cuộn dây thuần cảm L. Khi tần số dòng điện bằng 100Hz thì điện áp hiệu dụng U_R = 10V, U_AB = 20V và cường độ dòng điện hiệu dụng qua mạch là I = 0,1A. R và L có giá trị nào sau đây?

A. R = 100Ω; L = \(\sqrt{3}\) /(2π) H.                                 B. R = 100Ω; L = \(\sqrt{3}\) /π H.                                                

C. R = 200Ω ; L = 2/π H.                                           D. R = 200Ω; L =\(\sqrt{3}\) /π H.

Câu 5:Mạch RLC mắc nối tiếp, khi tần số dòng điện là f thì cảm kháng Z_L= 25(Ω) và dung kháng Z_C = 75(Ω) Khi mạch có tần số f0 thì cường độ dòng điện trong mạch đạt giá trị cực đại .Kết luận nào là đúng:

A. f₀ = \(\sqrt{3}\)f                   B. f =\(\sqrt{3}\) f₀                    C. f₀ = 25\(\sqrt{3}\)f               D. f = 25\(\sqrt{3}\)f₀

Câu 6: Cho mạch gồm điện trở R và cuộn dây thuần cảm L mắc nối tiếp, L thay đổi được. Điện áp hiệu dụng hai đầu mạch là U, tần số góc  ω = 200(rad/s). Khi L = L₁ = π/4(H) thì u lệch pha so với i góc  φ₁  và khi L = L₂ = 1/π (H) thì u lệch pha so với i góc φ₂ . Biết φ₁ + φ₂ = 90⁰. Giá trị của điện trở R là

A. 50Ω.                           B. 65Ω.                            C. 80Ω.                         D. 100Ω.

HD: Dùng công thức : tanφ₁ + tanφ₂ = sin(φ₁ + φ₂ )/ (cos φ_{1 .}cos φ₂ )

Câu 7 (CĐ 2007): Lần lượt đặt điện áp xoay chiều u = 5\(\sqrt{2}\)cos(ωt) với  ω không đổi vào hai đầu mỗi phần tử: điện trở thuần R, cuộn dây cảm thuần có độ tự cảm L, tụ điện có điện dung C thì dòng điện qua mỗi phần tử trên đều có giá trị hiệu dụng bằng 50 mA. Đặt điện áp này vào hai đầu đoạn mạch gồm các phần tử trên mắc nối tiếp thì tổng trở của đoạn mạch là

A.  3100Ω .                     B. 100 Ω.                        C.   2100Ω .                    D. 300 Ω.