Vật lý lớp 12
Bài tập dao động điều hòa hay và khó có lời giải chi tiết

Bài tập trắc nghiệm dao động điều hòa có lời giải chi tiết ( chọn lọc)

Cập nhật lúc: 14:45 16-04-2015 Mục tin: Vật lý lớp 12

Hệ thống bài tập trắc nghiệm dao động điều hòa hay và khó có lời giải chi tiết giúp các em hiểu sâu kiến thức lý thuyết và rèn luyện kỹ năng giải bài tập

Xem thêm:

Câu 1: Cho ba dao động điều hòa cùng phương, cùng tần số là x1 = \(10COS\left ( 2\pi t+\frac{\pi }{6} \right )\)cm, x2 = \(A_{2}COS\left ( 2\pi t-\frac{\pi }{2} \right )\) cm, x3 = \(A_{3}COS\left ( 2\pi t+\frac{7\pi }{6} \right )\) cm ( \(A_{3}\) < 10 cm). Khi đó dao động tổng hợp của ba dao động trên có phương trình là x = \(8COS\left ( 2\pi t+\varphi \right )\) cm. Giá trị của cực đại của A2 có thể nhận là:           

     A. 16 cm              B. \(\frac{8}{\sqrt{3}}\)  cm                     C. \(\frac{16}{^{\sqrt{3}}}\)  cm        D. \(8\sqrt{3}\)cm

  GIẢI:  

Ta  có x = x1 + x2 + x3 ( theo vectơ )

Ở đây ta dùng giản đồ vectơ Fresnel để biểu thị các dao động.

Mấu chốt nằm ở chỗ vectơ x1 và x3 ngược pha nhau           

nhưng biên độ \(A_{3}< 10\Rightarrow A_{3}< A_{1}\)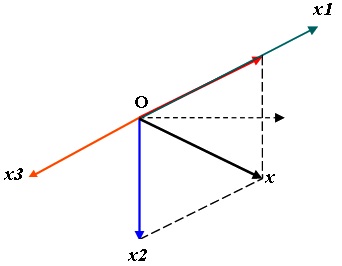                                      

Vậy sau khi tổng hợp x1 + x3 = x'

x4 = \(10-A_{3}COS\left ( 2\pi t+\frac{7\pi }{6} \right )\)

 Như vậy lúc này x = x2 + x4 ( theo vectơ )

Ta Lại có \(A^{2}={A_{2}}^{2}+{A_{4}}^{2}+2A_{2}A_{4}COS\left ( \varphi _{4}-\varphi _{ 2} \right )\)

 \(\Rightarrow {A_{3}}^{2}-\left ( 20-A_{2} \right )A_{3}+{A_{2}}^{2}+10A_{2}-64=0\)

 Xem \(A_{3}\) là ẩn, \(A_{2}\) là tham số thì để pt có nghiệm \(\Leftrightarrow \Delta \geq 0\)

 \(\Rightarrow \left ( 20-A_{2} \right )^{2}-4\left ( {A_{2}}^{2}+10A_{2}-64 \right )\geq 0\Leftrightarrow 3{A_{2}}^{2}\leq 56\Rightarrow A_{2}\leqslant \frac{16}{\sqrt{3}}\) VẬY \(A_{2}\) max khi \(A_{2}=\frac{16}{\sqrt{3}}\) \(\Rightarrow\) ĐÁP ÁN: C

Câu 2: Một con lắc lò xo có khối lượng m = 1kg dao động điều hòa với cơ năng E = 0,125J. Tại thời điểm ban đầu có vận tốc v = 0,25m/s và gia tốc \(a=-6,25\sqrt{3}\)  m/\(s^{2}\) . Gọi T là chu kỳ dao động của vật. Động năng con lắc tại thời điểm t = 7,25T là:    

     A. \(\frac{3}{28}\)  J               B.  \(\frac{3}{32}\) J                C. \(\frac{3}{29}\) J                       D. \(\frac{3}{27}\)  J

GIẢI:

Từ \(E=\frac{1}{2}m{v_{max}}^{2}\Rightarrow v_{max}=\sqrt{\frac{2E}{m}}=0,5\)

 Lại có \(\Rightarrow \frac{v^{2}}{{v_{max}}^{2}}+\frac{a^{2}}{{a_{max}}^{2}}=1\) với \(\left\{\begin{matrix}v=0,25m/s \\ v_{max}=0,5m/s \\ a=-6,25\sqrt{3}m/s^{2} \end{matrix}\right.\)  \(\Rightarrow a_{max}=12,5m/s^{2}\)

 

 Ta có \(\left\{\begin{matrix}a_{max}=A\omega ^{2}=12,5 \\ v_{max}=A\omega =0,5 \end{matrix}\right.\)                                                

 

 Tại thời điểm ban đầu ta có \(a=-6,25\sqrt{3}=-\omega ^{2}x\Rightarrow x=0,01\sqrt{3}cm\)

 

 Lập tỉ số \(\frac{X}{A}=cos\varphi =\frac{\sqrt{3}}{2}\Rightarrow \varphi = \frac{\pi }{6}\) hoặc \(\varphi =-\frac{\pi }{6}\)

 do \(v> 0\Rightarrow \varphi < 0\) \(\Rightarrow \varphi =-\frac{\pi }{6}\)

 

 Phương trình dao động của vật là x = 0,02cos(\(\omega\)t - \(\frac{\pi }{6}\) ) m

 

 Thay t = 7,25T vào phương trình ta được x = 0,01 \(\Rightarrow\) x = A/2 \(\Rightarrow W_{đ}=3W_{t}\Rightarrow W_{đ}=\frac{3E}{4}=\frac{3}{12}J\) 

ĐÁP ÁN: B

 

Câu 3: Hai con lắc đơn giống nhau có chu kỳ To. Nếu tích điện cho hai vật nặng các giá trị lần lượt là \(q_{1}\) và \(q_{2}\) , sau đó đặt hai con lắc trong một điện trường đều E hướng thẳng đứng xuống dưới thì chu kỳ dao động của hai con lắc lần lượt là \(T_{1}=5T_{0},T_{2}=\frac{5}{7}T_{0}\) . Tỉ số \(\frac{q_{1}}{q_{2}}\)  bằng:

     A. -1                   B. 7             C. -2                                D. 0,5

 GIẢI: Ta có công thức con lắc đơn trong điện trường đều là g' = g ± \(\frac{qE}{m}, \frac{T'}{T}=\sqrt{\frac{g}{g'}}\) 

 Khi \(T_{1}=5T_{0}\Rightarrow g_{1}=\frac{g}{25}< g\Rightarrow g_{1}=g-\frac{q_{1}E}{m}\) (do E giảm \(\Rightarrow q_{1}< 0\) ) \(\Rightarrow\) \(\frac{24}{25}=\frac{q_{1}E}{m}\) (1)

 Khi  \(T_{2}=\frac{5T_{0}}{7}\Rightarrow g_{2}=\frac{49g}{25}> g\Rightarrow g_{2}=g + \frac{q_{2}E}{m}\) (do E giảm \(q_{2}> 0\)) \(\Rightarrow \frac{24}{25}=\frac{q_{2}E}{m}\) (2)

 Từ (1) và (2) \(\Rightarrow\) \(\frac{q_{1}}{q_{2}}=-1\)

ĐÁP ÁN: A

Bạn đọc bài viết tại đây:



Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 - Xem ngay

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Bài liên quan
Gửi bài tập - Có ngay lời giải!