Giải bài tập va chạm

Câu 1 : Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang với chu kì T = 2π (s), vật nặng là một quả cầu có khối lượng m₁. Khi lò xo có chiều dài cực đại và vật m₁ có gia tốc – 2 cm/s² thì một quả cầu có khối lượng \(m_{2}=\frac{m_{1}}{2}\) chuyển động dọc theo trục của lò xo đến va chạm đàn hồi xuyên tâm với m₁ và có hướng làm cho lò xo bị nén lại. Vận tốc của m₂ trước khi va chạm \(3\sqrt{3}cm/s\). Khoảng cách giữa hai vật kể từ lúc va chạm đến khi m₁ đổi chiều chuyển động lần đầu tiên là

A: 3,63 cm                  B:  6 cm                     C:  9,63 cm           D:2,37cm

Giải: Biên độ dao động ban đầu của vât:  a_max = ω²A₀  \(; \omega =\frac{2\pi }{T}=\)  1 rad/s =>  A₀ = 2cm

  Vận tốc của hai vật ngay sau khi va chạm là v₁ và v₂:

   m₁v₁ + m₂v₂ = m₂v₀ (1) với v₀ = - \(3\sqrt{3}cm/s\)

  \(\frac{m_{1}{v_{1}}^{2}}{2}+\frac{m_{2}{v_{2}}^{2}}{2}=\frac{m_{2}{v_{0}}^{2}}{2}(2)\)

    2v₁ + v₂ = v₀ (1’) ;  \(2{v_{1}}^{2}+{v_{2}}^{2} ={v_{0}}^{2} (2')\) 

Từ (1’) và (2’) :\(v_{1}=2\frac{v_{0}}{3}=-2\sqrt{3}cm/s; v_{2}=-\frac{v_{0}}{3}=\sqrt{3}cm/s\)

 Biên độ dao động của m₁ sau va chạm:  A² = A₀² + \(\frac{{v_{1}}^{2}}{\omega ^{2}}\).= 0,02² + (0,02\(\sqrt{3}\))² = 0,0016 (m²)

 => A = 0,04 m = 4cm. Thời gian từ lúc va chạm đến khi m₁ đổi chiều chuyển động lần đầu tiên tức khi m₁ ở vị trí biên âm; ( vật đi từ li độ \(\frac{A}{2}\)  đến li độ -A)  \(t=\frac{T}{12}+\frac{T}{4}=\frac{T}{3}=\frac{2\pi }{3}=2,1s\)

Quáng đường vật m₁ đi được   S₁ = 1,5A = 6cm

Sau va chạm m₂ quay trở lại và đi được quãng đường S₂ = v₂t = \(\sqrt{3}\).2,1 = 3,63 cm

Khoảng cách giữa hai vật kể từ lúc va chạm đến khi m₁ đổi chiều chuyển động lần đầu tiên là

  S = S₁ + S₂ = 9,63cm.

=>Đáp án C 

 Câu  2 Một vật nhỏ có khối lượng M = 0,9 (kg), gắn trên một lò xo nhẹ thẳng đứng có độ cứng 25(N/m) đầu dưới của lò xo cố định. Một vật nhỏ có khối lượng m=0,1 (kg) chuyển động theo phương thẳng đứng với tốc độ \(0,2\sqrt{2}\) m/s đến va chạm mềm với M. Sau va chạm hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường g=10m/s². Biên độ dao động là:

    A 4,5 cm            B 4 cm            C \(4\sqrt{2}\) cm       D \(4\sqrt{3}cm\) 

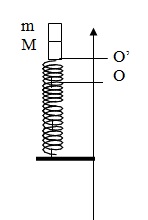
Giải:  Vận tốc của hai vật sau va chạm:  (M + m)V = mv   

=>  V = 0,02\(\sqrt{2}\)  (m/s)

Tọa độ ban đầu của hệ hai vật  x₀ =\(\frac{(M+m-M)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm

\(A^{2}={x_{0}}^{2}+\frac{V^{2}}{\omega ^{2}}={x_{0}}^{2}+\frac{V^{2}(M+m)}{k}=0,0016\Rightarrow A=0,04m=4cm\)

  Đáp án B

  Câu 3 : Con lắc lò xo gồm vật nặng M = 300g, lò xo có độ cứng k = 200N/m, lồng vào một trục thẳng đứng như hình vẽ. Khi M đang ở vị trí cân bằng thì vật m = 200g từ độ cao h = 3,75cm so với M rơi tự do, va chạm mềm với M, coi ma sát là không đáng kể, lấy g = 10m/s² Sau va chạm hai vật cùng dao động điều hòa, chọn gốc tọa độ tại vị trí cân bằng của hệ, chiều dương như hình vẽ, góc thời gian t = 0 là lúc va chạm. Phương trình dao động của hệ hai vật là 

A. x = 1,08cos(20t + 0,387)cm.           B. x = 2,13cos(20t + 1,093)cm.
C. x = 1,57cos(20t + 0,155)cm.           D. x = 2cos(20t + \(\frac{\pi }{3}\)) cm.

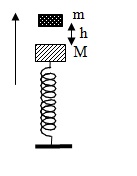
Giải: Vận tốc của vật m khi va chạm vào M

   \(v=\sqrt{2gh}\)

Vận tốc v₀ của hệ hai vật sau va chạm:

  (M+m)v₀  = mv => v₀ =  \(\frac{m\sqrt{2gh}}{M+m}\) 

Khi đó vị trí của hệ hai vật cách vị trí cân bằng của hệ

  x₀ = ∆l -  ∆l₀ =\(\frac{(M+m)-M}{k}g=\frac{m}{k}g\)  = 0,01m = 1cm

Biên độ dao động của hệ:  A² = x₀² + \(\frac{{v_{0}}^{2}}{\omega ^{2}}\)

  Với   \(\omega =\sqrt{\frac{k}{M+m}}=\sqrt{\frac{200}{0,5}}\)= 20 (rad/s)

  A =\(\sqrt{{x_{0}}^{2}+\frac{{v_{0}}^{2}}{\omega ^{2}}}=\sqrt{0,01^{2}+\frac{0,12}{20^{2}}}\) = 0,02 m = 2cm

Phương trình dao động của hệ hai vật   x = Acos(20t +φ)

khi t = 0 =>  x = x₀ = A/2 => cosφ = 0,5  \(\Rightarrow \varphi =\frac{\pi }{3}\)

=> x = 2cos(20t + \(\frac{\pi }{3}\)) cm.

=> Đáp án D

Bạn đọc tải file đính kèm tại đây: